[python] 평가 (정확도, 오차행렬, 정밀도, 재현율)
2021. 5. 6. 15:32ㆍPython/문법
3.1_3-5_정확도 _ ROC_AUC 예제.ipynb
0.11MB
Ver. Jupyter Notebook (Anaconda3)
▶ 정확도
정확도 = 예측 결과가동일한 데이터 건수 / 전체 예측 데이터 건수
# 이진 분류 시 좋은 평가 지표는 아니다.
# 예) 0~10 숫자 중 0일 경우를 맞추는 문제에서, 모든 답을 아니라고 하면 정확도는 90%가 됨
더보기
>>> from sklearn.datasets import load_digits # mnist 데이터셋 로드
>>> from sklearn.model_selection import train_test_split
>>> from sklearn.base import BaseEstim
>>> from sklearn.metrics import accuracy_score
>>> import numpy as np
>>> import pandas as pd
# 모든 데이터를 0으로 만드는 클래스
>>> class MyFakeClassifier(BaseEstimator):
>>> def fit(self, X, y):
>>> pass
# 입력값으로 들어오는 X 데이터 셋의 크기만큼 모두 0값으로 만들어서 반환
>>> def predict(self, X):
>>> return np.zeros( (len(X), 1) , dtype=bool)
# 사이킷런의 내장 데이터 셋인 load_digits( )를 이용하여 MNIST 데이터 로딩
>>> digits = load_digits()
>>> digits
{'data': array([[ 0., 0., 5., ..., 0., 0., 0.],
[ 0., 0., 0., ..., 10., 0., 0.],
[ 0., 0., 0., ..., 16., 9., 0.],
...,
[ 0., 0., 1., ..., 6., 0., 0.],
[ 0., 0., 2., ..., 12., 0., 0.],
[ 0., 0., 10., ..., 12., 1., 0.]]),
'target': array([0, 1, 2, ..., 8, 9, 8]),
'frame': None,
'feature_names': ['pixel_0_0',
'pixel_0_1',
'pixel_0_2',
'pixel_0_3',
# mnist의 feature 데이터
>>> print(digits.data.shape)
>>> digits.data
(1797, 64)
array([[ 0., 0., 5., ..., 0., 0., 0.],
[ 0., 0., 0., ..., 10., 0., 0.],
[ 0., 0., 0., ..., 16., 9., 0.],
...,
[ 0., 0., 1., ..., 6., 0., 0.],
[ 0., 0., 2., ..., 12., 0., 0.],
[ 0., 0., 10., ..., 12., 1., 0.]])
# mnist의 target 데이터
>>> print(digits.target.shape)
>>> digits.target
(1797,)
array([0, 1, 2, ..., 8, 9, 8])
# 7번이면 True이고 1로 변환, 7번이 아니면 False이고 0으로 변환
>>> y = (digits.target == 7).astype(int)
>>> y
array([0, 0, 0, ..., 0, 0, 0])
# train, test 데이터 분리
>>> X_train, X_test, y_train, y_test = train_test_split(digits.data, y, random_state=11)
# InteractiveShell : print 안 써도 쉘의 모든 결과를 출력해주는 라이브러리
>>> from IPython.core.interactiveshell import InteractiveShell
>>> InteractiveShell.ast_node_interactivity = "all"
>>> X_train.shape
>>> y_train.shape
(712, 8)
(712,)
>>> X_test.shape
>>> y_test..shape
(450, 64)
(450,)
# 불균형한 레이블 데이터 분포도 확인.
>>> print('레이블 테스트 세트 크기 :', y_test.shape, '\n')
>>> print('테스트 세트 레이블 0(7이 아닌 숫자)과 1(숫자 7)의 분포도')
>>> print(pd.Series(y_test).value_counts())
레이블 테스트 세트 크기 : (450,)
테스트 세트 레이블 0(7이 아닌 숫자)과 1(숫자 7)의 분포도
0 405
1 45
dtype: int64
# MyFakeClassifier(모든 숫자 예측을 0으로(7이 아니다) 하는 모델)로 학습 및 예측
>>> fakeclf = MyFakeClassifier()
>>> fakeclf.fit(X_train , y_train)
# 정확도 평가
>>> fakepred = fakeclf.predict(X_test)
>>> print('모든 예측을 0으로 하여도 정확도는:{:.3f}'.format(accuracy_score(y_test , fakepred)))
모든 예측을 0으로 하여도 정확도는:0.900
▶ 오차 행렬
| 예측 클래스 (Predicted Class) |
|||
| 실제 클래스 (Actual Class) |
Negative(0) | Positive(1) | |
| Negative(0) | TN (True Negative) |
FP (False Positive) |
|
| Positive(1) | FN (False Negative) |
TP (True Positive) |
|
더보기
>>> from sklearn.metrics import confusion_matrix
# 예측 결과 fakepred와 실제 결과 y_test의 Confusion Matrix출력
>>> confusion_matrix(y_test , fakepred)
array([[405, 0],
[ 45, 0]], dtype=int64)
▶ 정밀도, 재현율의 관계
정밀도 = TP / (FP + TP)
재현율 = TP / (FN + TP)

# 암에 걸렸을 확률 같은 경우 임계값을 낮게 잡아 재현율을 높이는것이 유리
# 스펨 메일같은 경우 임계값을 높여 중요한 메일이 스팸으로 걸러지는 것을 방지하는 것이 좋음
더보기
>>> from sklearn.metrics import accuracy_score, precision_score , recall_score
>>> print("정밀도:", precision_score(y_test, fakepred))
>>> print("재현율:", recall_score(y_test, fakepred))
정밀도: 0.0
재현율: 0.0
# 오차행렬, 정확도, 정밀도, 재현율을 한꺼번에 계산하는 함수 생성
>>> from sklearn.metrics import accuracy_score, precision_score , recall_score , confusion_matrix
# confusion matrix, accuracy, precision, recall을 한꺼번에 계산하는 함수
>>> def get_clf_eval(y_test , pred):
>>> confusion = confusion_matrix( y_test, pred)
>>> accuracy = accuracy_score(y_test , pred)
>>> precision = precision_score(y_test , pred)
>>> recall = recall_score(y_test , pred)
>>> print('오차 행렬')
>>> print(confusion)
>>> print('정확도: {0:.4f}, 정밀도: {1:.4f}, 재현율: {2:.4f}'.format(accuracy , precision ,recall), '\n')
# 타이타닉 데이터에 로직스틱 회기 모델로 이진 분류한 후에 오차행렬, 정확도, 정밀도, 재현율 구해보기
>>> import numpy as np
>>> import pandas as pd
>>> from sklearn.model_selection import train_test_split
>>> from sklearn.linear_model import LogisticRegression
# 타이타닉 데이터 로드
>>> titanic_df = pd.read_csv('./titanic_train.csv')
# feature(X), target(y) 데이터 분리
>>> y_titanic_df = titanic_df['Survived']
>>> X_titanic_df= titanic_df.drop('Survived', axis=1)
# 데이터 전처리
>>> X_titanic_df = transform_features(X_titanic_df)
# train, test 데이터 분리
>>> X_train, X_test, y_train, y_test = train_test_split(X_titanic_df, y_titanic_df, \
test_size=0.20, random_state=11)
# 로지스틱 회귀(분류 모델) 모델 정의
>>> lr_clf = LogisticRegression()
>>> lr_clf
LogisticRegression()
# 학습
>>> lr_clf.fit(X_train , y_train)
# 예측
>>> pred = lr_clf.predict(X_test)
# 평가지표 계산
>>> get_clf_eval(y_test , pred)
오차 행렬
[[104 14]
[ 13 48]]
정확도: 0.8492, 정밀도: 0.7742, 재현율: 0.7869
# F1 Score와 ROC Curve, AUC가 가장 많이 사용됨
▶ F1 Score
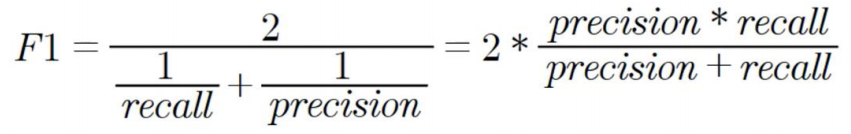
더보기
>>> from sklearn.metrics import f1_score
# f1_score 클래스를 이용해서 f1 score 계산
>>> f1 = f1_score(y_test , pred) # 실제값, 예측값
>>> print('F1 스코어: {0:.4f}'.format(f1))
F1 스코어: 0.7805
>>> def get_clf_eval(y_test , pred):
>>> confusion = confusion_matrix( y_test, pred)
>>> accuracy = accuracy_score(y_test , pred)
>>> precision = precision_score(y_test , pred)
>>> recall = recall_score(y_test , pred)
# F1 스코어 추가
>>> f1 = f1_score(y_test,pred)
>>> print('오차 행렬')
>>> print(confusion)
# f1 score print 추가
>>> print('정확도: {0:.4f}, 정밀도: {1:.4f}, 재현율: {2:.4f}, F1:{3:.4f}'.format(accuracy, precision, recall, f1), '\n')
>>> thresholds = [0.4 , 0.45 , 0.50 , 0.55 , 0.60]
>>> pred_proba = lr_clf.predict_proba(X_test)
# 분류 임계값 변경을 하면서 f1 score를 포함한 평가지표 확인
>>> get_eval_by_threshold(y_test, pred_proba[:,1].reshape(-1,1), thresholds)
임곗값: 0.4
오차 행렬
[[98 20]
[10 51]]
정확도: 0.8324, 정밀도: 0.7183, 재현율: 0.8361, F1:0.7727
임곗값: 0.45
오차 행렬
[[103 15]
[ 12 49]]
정확도: 0.8492, 정밀도: 0.7656, 재현율: 0.8033, F1:0.7840
임곗값: 0.5
오차 행렬
[[104 14]
[ 13 48]]
정확도: 0.8492, 정밀도: 0.7742, 재현율: 0.7869, F1:0.7805
임곗값: 0.55
오차 행렬
[[109 9]
[ 15 46]]
정확도: 0.8659, 정밀도: 0.8364, 재현율: 0.7541, F1:0.7931
임곗값: 0.6
오차 행렬
[[112 6]
[ 16 45]]
정확도: 0.8771, 정밀도: 0.8824, 재현율: 0.7377, F1:0.8036
# 위 데이터의 경우 임계값이 0.6일 때 f1 score가 가장 높다. 그런데 재현율이 너무 낮기 때문에 여러가지 요소를 고려해야 한다.
▶ ROC Curve와 AUC
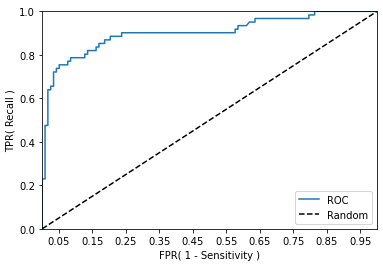
# ROC Curve : 파란색 곡선
# AUC : ROC Curve를 기준으로 아래쪽 면적
# AUC가 높을 수록 좋은 결과 값
더보기
>>> from sklearn.metrics import roc_curve
# 레이블 값이 1일때의 예측 확률을 추출
>>> pred_proba_class1 = lr_clf.predict_proba(X_test)[:, 1]
>>> print(len(pred_proba_class1))
>>> pred_proba_class1[:20]
179
array([0.53815943, 0.12133005, 0.12283041, 0.11734445, 0.14489353,
0.11774417, 0.11157936, 0.79123724, 0.21729086, 0.63044738,
0.10017 , 0.12507789, 0.1228364 , 0.11162534, 0.56354548,
0.14104185, 0.09631462, 0.26666825, 0.27536599, 0.82819347])
# fpr, tps, thresholds
>>> fprs , tprs , thresholds = roc_curve(y_test, pred_proba_class1)
>>> print('분류 임곗값 Shape :', thresholds.shape, '\n')
분류 임곗값 Shape : (55,)
# 반환된 임곗값 배열 로우가 55건이므로 샘플로 10건만 추출하되, 임곗값을 5 Step으로 추출.
>>> thr_index = np.arange(0, thresholds.shape[0], 5)
>>> print('샘플 추출을 위한 임곗값 배열의 index 10개:', thr_index)
>>> print('샘플용 10개의 임곗값: ', np.round(thresholds[thr_index], 2))
샘플 추출을 위한 임곗값 배열의 index 10개: [ 0 5 10 15 20 25 30 35 40 45 50]
샘플용 10개의 임곗값: [1.97 0.75 0.63 0.59 0.49 0.4 0.35 0.23 0.13 0.12 0.11]
# 5 step 단위로 추출된 임계값에 따른 FPR, TPR 값
>>> print('샘플 임곗값별 FPR: ', np.round(fprs[thr_index], 3))
>>> print('샘플 임곗값별 TPR: ', np.round(tprs[thr_index], 3))
샘플 임곗값별 FPR: [0. 0.017 0.034 0.051 0.127 0.161 0.203 0.331 0.585 0.636 0.797]
샘플 임곗값별 TPR: [0. 0.475 0.689 0.754 0.787 0.836 0.869 0.902 0.918 0.967 0.967]
>>> from sklearn.metrics import roc_auc_score
>>> pred_proba = lr_clf.predict_proba(X_test)[:, 1]
>>> roc_score = roc_auc_score(y_test, pred_proba)
>>> print('ROC AUC 값: {0:.4f}'.format(roc_score))
ROC AUC 값: 0.9024
'Python > 문법' 카테고리의 다른 글
| [python] 텍스트 분석 (0) | 2021.05.11 |
|---|---|
| [python] 분류 (0) | 2021.05.07 |
| [Python] 데이터 전처리 (원-핫 인코딩, 표준화, 정규화) (0) | 2021.05.05 |
| [python] 사이킷런으로 머신러닝 (0) | 2021.05.04 |
| [python] numpy (0) | 2021.05.03 |

